In a paper published in the Journal of Environmental Management, researchers explored the challenges of planning under complex uncertainty using traditional exploration methods, which struggled to enable autonomous adaptation, necessitating additional efforts to finalize adaptive plans and compromising decision-making efficiency. They introduced reinforcement learning (RL) as a new exploration method integrating closed-loop control, enabling automated adaptive policy-making in uncertain planning scenarios.
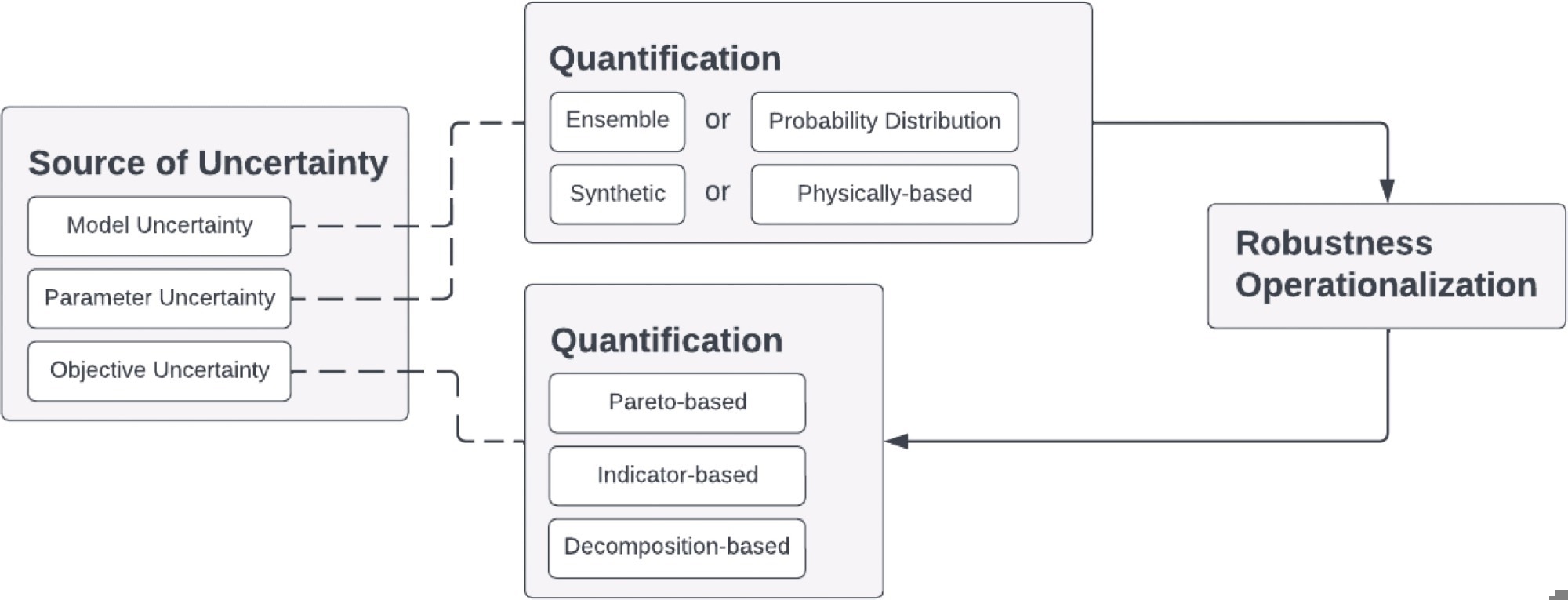A general process for uncertainty characterization, adapted from Herman et al. (2020) and Kwakkel et al. (2015). In this process, the model and parameter uncertainties are first quantified. Then, the results are collected for robustness operationalization. Eventually, the objective uncertainty is quantified based on the robustness operationalization results. Image Credit: https://www.sciencedirect.com/science/article/pii/S030147972400954X
Comparing RL with the multi-objective evolutionary algorithm (MOEA) through computational experiments on two hypothetical problems, they found RL consistently demonstrated superior efficiency and robust policy adaptation, leveraging its exploration history. At the same time, MOEA excelled in intuitively quantifying objective uncertainty, enhancing robustness against objective variability, and providing valuable guidance for researchers in selecting appropriate exploration methods tailored to specific application contexts.
Related Work
Previous research explored multi-objective robust optimization methods, such as MOEA and multiple criteria decision-making (MCDM), for decision-making under deep uncertainty (DMDU). MOEA evolves solutions iteratively to approximate the Pareto frontier, while MCDM transforms multi-objective problems into single-objective ones using scalarizing functions. RL searches for optimal policies through trial and error, utilizing Markov decision processes (MDPs) and various exploration and evaluation strategies within the agent-environment framework.
Experiment Overview Summary
This study conducted experiments comparing two RL algorithms, multi-objective natural evolution strategy (MO-NES) and multi-objective extension of relative entropy policy search (MO-eREPS), with a baseline MOEA. Specifically, Epsilon-dominance non-dominated sorted genetic algorithm II (-NSGA-II), in two deeply uncertain environmental management case studies to showcase the efficacy of RL in DMDU and its synergies with existing exploratory modeling methods, t. The team opted for MOEA as the baseline due to its widespread adoption in DMDU. The selected RL algorithms, inner-loop multi-policy MORL algorithms, share characteristics with MOEA, facilitating direct comparison.
The case studies encompassed the water reservoir control problem and the lake problem, two prototypical scenarios in MORL and DMDU, respectively. The water reservoir control problem involves managing annual water release from a reservoir to balance flood prevention with downstream water and electricity demands.
In contrast, the lake problem entails optimizing pollution emissions to maximize economic benefits while averting irreversible lake eutrophication. Both issues featured discrete action spaces, aligning with common planning contexts and streamlining computation.
In the water reservoir control problem, analysts adapted the original model, modeling parameters, and objectives while considering uncertainties such as initial water volume and annual natural water inflow. The lake problem incorporated uncertain parameters like pollution removal rate and natural pollution inflow alongside objectives including average pollution concentration and economic benefit. Despite the popularity of the lake problem in DMDU studies, its suitability for evaluating methods has been questioned due to its limited trade-offs and stochastic uncertainties.
Uncertainty characterization involves synthetically generating scenario ensembles to quantify model and parameter uncertainties for all algorithms. Robustness operationalization measured policy performance across scenarios, mapping it to scalar values using robustness metrics. Based on these results, objective uncertainty was quantified employing Pareto-based, indicator-based, and decomposition-based methods. RL algorithms MO-NES and MO-eREPS adopted indicator-based approaches, while NSGA-II followed Pareto-based approaches.
The evaluation focused on computational efficiency and policy robustness, with RL algorithms trained iteratively for convergence and -NSGA-II trained for a fixed number of functional assessments. Policies were sampled and evaluated across scenario ensembles, and their robustness was assessed using hypervolume computation. The team meticulously designed the experimental settings to ensure reproducibility and separately assess algorithm performance under various uncertainties. Each experiment was run multiple times with different random seeds to test algorithm stability against randomness.
RL Policy Adaptability
In the conducted experiments, RL policies demonstrated notable adaptability, enhancing their performance in DMDU by adjusting to real-time conditions during deployment. MO-NES and MO-eREPS consistently exhibited significantly higher computational efficiency and policy robustness than the baseline MOEA (-NSGA-II).
For the multi-objective water reservoir control problem, RL algorithms outperformed NSGA-II in computational efficiency, being around six times faster with 1 central processing unit (CPU) compared to NSGA-II with 75 CPUs. Despite similar policy robustness, RL algorithms consistently provided higher average hypervolume and lower standard deviations, indicating better average policy robustness and stability against randomness.
RL algorithms remained more computationally efficient in the more complex multi-objective lake problem, being around 4 times faster than -NSGA-II with 1 CPU compared to 75 CPUs. However, -NSGA-II outperformed RL algorithms in average hypervolume, though RL algorithms showed lower hypervolume standard deviations.
Despite this, RL algorithms offered a wider range of trade-offs across objectives, complementing -NSGA-II. The hypervolume metric needed to be revised, as it needed to capture the nuanced policy performance distributions fully. The RL algorithms' advantage became more pronounced in parameter uncertainty, where they exhibited significantly higher average hypervolume and provided more diverse trade-offs across objectives, especially when using the mean for robustness operationalization.
Conclusion
In summary, this paper introduced RL as a novel multi-objective robust optimization method for exploratory analysis within DMDU approaches, aiming to supplement existing methodologies lacking self-adaptation capabilities. A comparative study with MOEA identified two RL algorithms consistently providing higher computational efficiency and policy robustness in parameter uncertainty scenarios.
Discussions emphasized the importance of RL's exploration strategy, highlighting its efficacy in leveraging available information compared to MOEA. Future research directions include exploring RL algorithms against state-of-the-art methods beyond MOEA and investigating their performance in many-objective optimization problems, addressing the limitations of the lake problem as a case study in DMDU.
Why "Open" AI Often Means More Power for Tech Giants