Accelerating Electrodynamics with ML: The FoHM-NO Method

By Dr Silpaja Chandrasekar, PhDReviewed by Susha Cheriyedath, M.Sc.Jul 5 2024

In a paper published in the journal Scientific Reports, researchers introduced the Fourier–Helmholtz–Maxwell neural operator (FoHM-NO) method, using a Fourier transformation (FT)-based representation of Maxwell’s equations for electrodynamics without gauge ambiguity. This method integrated Gauss’s laws, Faraday’s law, and the longitudinal component of Ampère–Maxwell in Fourier space as strict constraints.

Using an encoder-decoder network, it predicted electromagnetic (EM) fields from the FT vector potential transverse components. Tested on electron beam simulations, the u-shaped network (U-Net) architecture trained faster, achieved higher accuracy, and demonstrated superior generalization compared to other models, effectively accelerating the solution of Maxwell’s equations.

Related Work

Past work has shown that machine learning (ML) methods can enhance simulations and measurements in electrodynamics, but calculating relativistic charged particle dynamics remains challenging. Conventional methods like particle-in-cell and point-to-point CSR calculations are computationally intensive, especially for large particle collections. Recent advances include enforcing hard physics constraints in ML models to improve generalization, though they introduce gauge ambiguity.

Efficient EM Simulation

The formalism used in this study, also employed in the canonical quantization of the electromagnetic field, is designed to minimize the number of fields needed to model while ensuring many of Maxwell’s equations are satisfied as hard constraints. The team started with Maxwell’s equations in position space, performed a 3D spatial Fourier transform, and rewrote them in Fourier space. It separates vector components into those longitudinal and transverse to the wave vector. By doing so, Gauss’s law for the electric and magnetic fields, Faraday’s law, and the transverse components of the Ampère–Maxwell equation can be expressed and handled more efficiently.

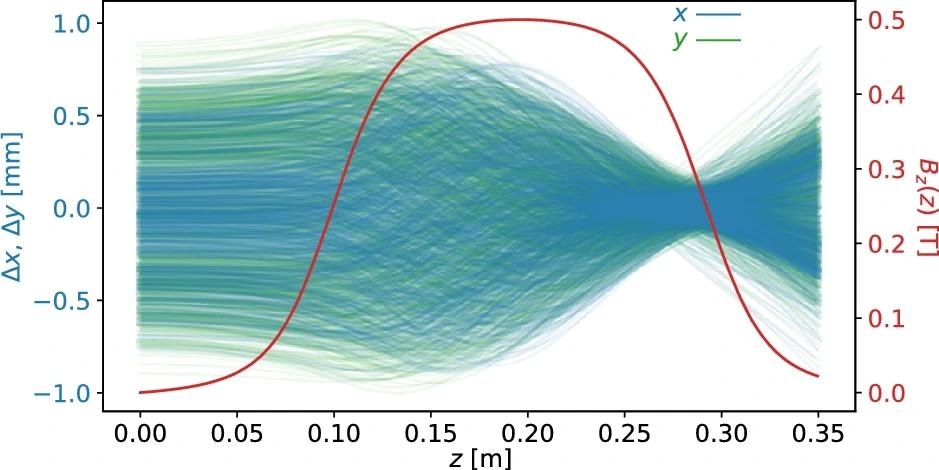The (x, y) trajectories of 1000 random electrons within the beam are shown along with the z-component of the 0.5 Tesla magnetic field of the solenoid which over-compresses the beam. Image Credit: https://www.nature.com/articles/s41598-024-65650-9

The EM fields can be determined using the FoHM-NO method, given charge and current density distributions. This method incorporates Fourier transformations, Helmholtz decompositions, and Maxwell’s equations within a neural operator framework.

Specifically, it uses convolutional neural networks to estimate the EM fields from the transverse components of the vector potential, ensuring that several of Maxwell’s equations are automatically satisfied as hard constraints. This approach leverages the fact that the EM fields have only two independent degrees of freedom, simplifying the modeling process and reducing computational complexity.

The FoHM-NO method offers several advantages: it bypasses gauge redundancy by focusing on transverse components of the vector potential, simplifies spatial derivatives and constraints in Fourier space, and leverages fast Fourier transforms for efficient computations, even with large datasets. While this study does not incorporate spatial boundary conditions, it demonstrates potential in predicting EM fields from charged particle beams and other EM scenarios.

Despite potentially lower accuracy than state-of-the-art methods, its rapid runtime benefits time-sensitive applications like accelerator control. Further developments could expand its use to include matter density fields, enhancing its versatility and practical utility in solving complex EM problems.

U-Net Superiority and Adaptability

In evaluating various models across different datasets, the U-Net consistently outperformed smaller convolutional neural networks (CNNs) and a larger CNN model in terms of accuracy and generalization. The U-Net consistently achieved lower errors across training, validation, and test datasets, demonstrating superior performance in maintaining minimal errors compared to other models as validation progressed. It highlights the efficiency and effectiveness of the U-Net architecture in predictive modeling for complex electromagnetic field simulations. Transfer learning was employed to enhance the U-Net's performance on new beam configurations not seen during initial training.

After retraining on the first 85% of the Gaussian beam dataset, the U-Net demonstrated remarkable improvement with just 20 additional epochs, achieving performance comparable to its original results on the complex beam. It underscores the effectiveness of the approach in adapting to new datasets and configurations, showcasing robust generalization capabilities. These results emphasize the robustness and adaptability of the U-Net model in handling complex electromagnetic field predictions across varied datasets.

By leveraging transfer learning and expanding the training data to include additional beam configurations, the U-Net consistently improved its predictive accuracy, demonstrating its potential for practical applications in diverse experimental setups and accelerating the development of reliable predictive models in accelerator physics and related fields.

Conclusion

To sum up, a novel approach applied ML to EM problems using Maxwell’s equations in Fourier space. This method incorporated several of Maxwell’s equations as hard constraints, enhancing the physical plausibility of the output. The FoHM-NO method proved advantageous in computational EM scenarios by prioritizing speed and achieving significant acceleration at the cost of a minor increase in error. The U-Net architecture emerged as the top performer in field recreation and generalization beyond training data. Though these approaches are still early, integrating domain-specific physics constraints into ML tools showed promise.